R

첫 번째(그리고 아마도 더 흔한) 반복문은 for 반복문이다. 이 반복문은 어떤 작업을 정해진 횟수만큼 수행할 때 특히 유용하다. 이제 간단한 for 반복문 예제를 살펴본 뒤 코드의 문법에 대해 논의해 보자.

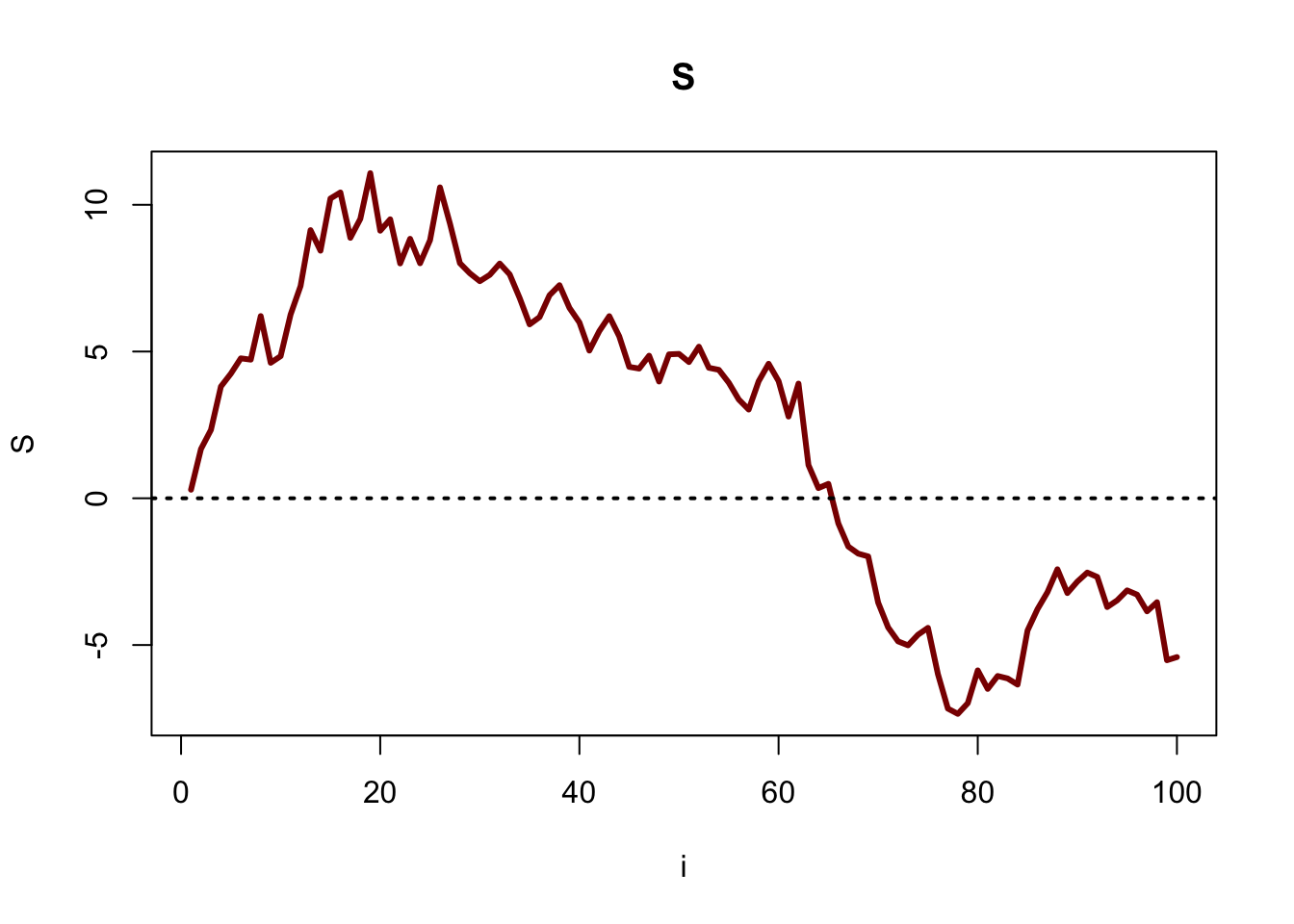
이제 코드를 단계별로 살펴보자.set.seed() 함수는 작업을 재현할 수 있도록 해준다. 즉, 컴퓨터는 실제로는 완전한 무작위성을 가지지 않고 ‘의사난수(pseudo-random)’ 과정을 사용한다. 따라서 ‘시드(seed)를 설정한다’는 것은 동일한 ‘무작위’ 과정을 여러 번 똑같이 생성할 수 있도록 해주는 것이다. 그 다음 코드인 S = rep(NA, 100)은 우리가 값을 채워 넣을 경로(path)를 미리 설정하는 것이다. 보통은 벡터를 실제 값으로 채우기 전에 NA로 초기화하는 것이 좋은 습관이다. 다음으로 첫 번째 값을 정의해야 한다. S[1] = rnorm(1, 0, 1)이라는 코드로 이를 설정한다. 이 값은 다른 값들과는 조금 다르다. 왜냐하면 i=1일 때 S_i−1은 S₀=0 이기 때문이다. 따라서 S₁ ​을 얻기 위해서는 단순히 $N(0,1)$에서 난수를 하나 추출하면 된다. 마지막으로 루프에 들어가 보자. 이미 S[1]은 채워 넣었으므로, 이제 S[2]부터 S[100]까지 채워야 한다. 따라서 i가 2에서 100까지 증가해야 하고, 그래서 for 반복문에 for (i in 2:100)이라고 쓰는 것이다. 그 안에서 우리는 S_i​를 생성한다. 방법은 이전 값 S_i−1​에 $N(0,1)$에서 새로 뽑은 난수 하나를 더하는 것이다. i는 매번 루프를 돌 때마다 1씩 증가하므로, 코드에서는 S[i - 1]과 S[i]를 다루게 된다. 예를 들어, i=50일 때 $S[50]$을 구하려면, rnorm(1, 0, 1)을 통해 $N(0,1)$에서 난수 하나를 뽑고, 이를 S[49]에 더하면 된다. 마지막 줄은 단순히 우리가 만든 데이터를 시각화하는 plot 함수이다. R에서 그래프를 그리는 방법은 이번 장의 뒷부분에서 더 자세히 배우게 될 것이다.

while loop

이들은 for 반복문과 매우 유사하지만, 하나의 근본적인 차이가 있다. for 반복문은 인덱스가 증가하는 동안 정해진 횟수만큼 실행되는 반면(보통 인덱스로 i를 사용한다), while 반복문은 ‘특정 조건이 만족되는 동안’ 실행된다. 다음 예제를 보자.

Plot()

plot() 함수는 가장 일반적이고 기본적인 그래프 함수이다. 이를 이용하면 산점도, 선 그래프 등을 만들 수 있고, 다양한 입력값을 통해 그래프를 자유롭게 커스터마이즈할 수 있다. 다음의 플롯을 예로 들어보자.

#define vectors
x = 1:10
y = x^2

#create the plot
plot(x, y,
     main = "Our First Plot!",
     xlab = "x",
     ylab = "y",
     xlim = c(0, 10),
     ylim = c(0, 100),
     type = "l",
     lwd = 5,
     col = "darkred")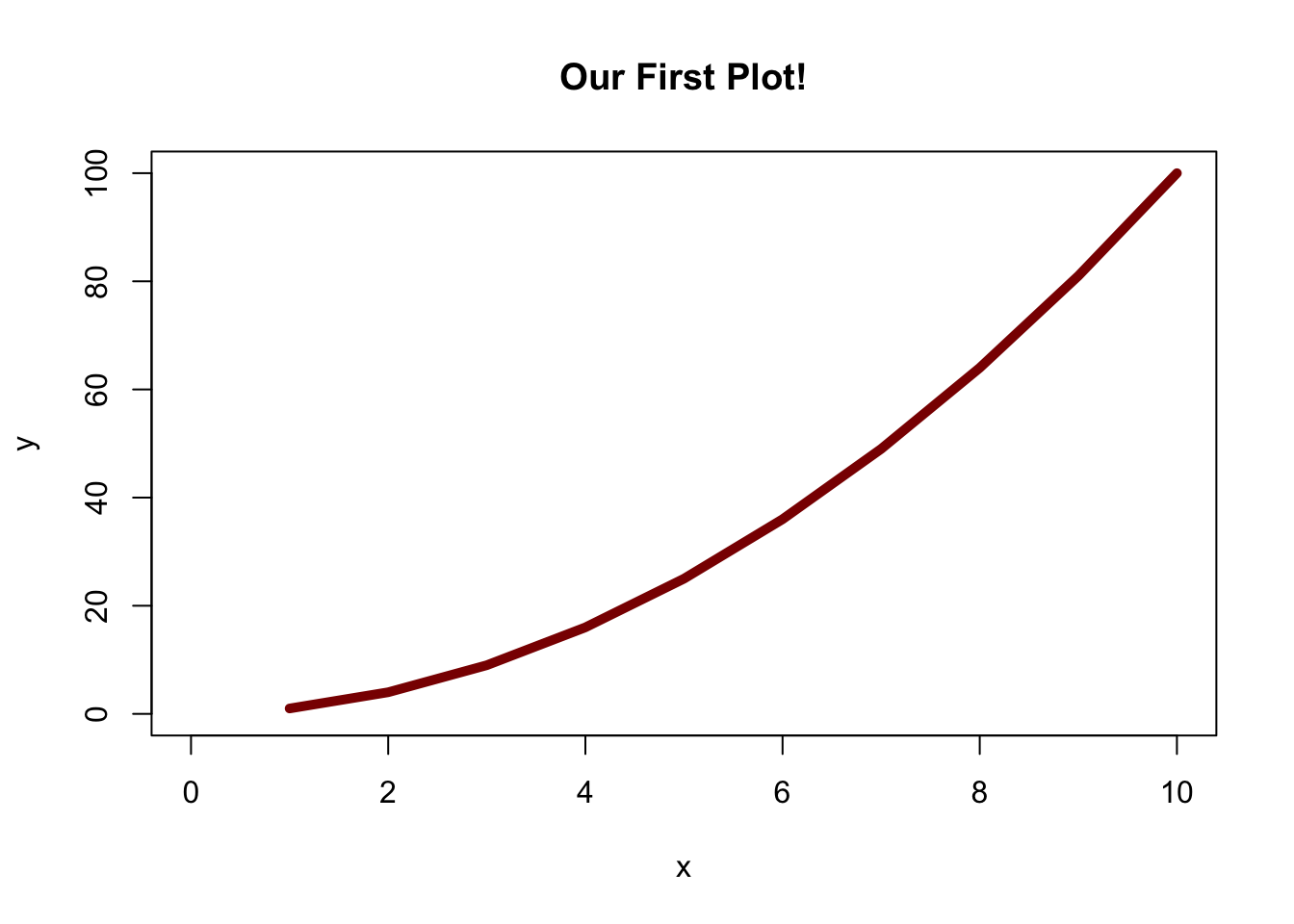

코드를 단계별로 살펴보자. 우선, plot 함수의 각 인자를 새 줄에 나누어 적었는데, 이는 사람이 코드를 읽고 이해하기 쉽게 하기 위함이다. 가장 앞의 두 인자이자 가장 중요한 인자는 x와 y인데, 이는 plot 함수가 x값과 y값을 각각 좌표로 하여 그래프를 그리도록 지시한다 (여기서는 y = x²). main 인자는 그래프의 제목을 정하는 역할을 한다. xlab과 ylab 인자는 각각 그래프의 x축과 y축의 이름을 정한다. 이 인자들과 main 인자 모두 문자열을 따옴표로 묶어서 전달해야 한다는 점에 유의해야 한다. xlim과 ylim 인자는 각각 x축과 y축의 범위를 설정한다. 이때 최소값과 최대값을 묶어서 전달해야 하므로 c() 함수를 사용한다 (c는 ‘concatenate’의 줄임말이다). type 인자는 그래프의 형태를 지정한다. 여기서는 l을 사용하여 선 그래프를 그렸지만, p를 쓰면 점 그래프, h를 쓰면 세로 막대 형태로 그릴 수도 있다. lwd 인자는 선의 두께를 지정한다. 값이 클수록 선이 두꺼워진다. col 인자는 선의 색상을 지정한다. R에서 사용할 수 있는 다양한 색상은 별도의 색상 데이터베이스를 참고할 수 있다. plot 함수와 유사하게, hist 함수를 이용하면 히스토그램도 그릴 수 있다. 도움말 페이지를 보면 자세한 내용을 확인할 수 있으며, 많은 인자들이 plot 함수와 동일하다.

Plotting Techniques

기본적인 plot 함수를 확장하는 데 도움이 되는 몇 가지 흥미로운 도구가 있다. 먼저, 다음 코드를 살펴보자.

#plot on a 3x3 grid
par(mfrow = c(3,3))
#run the loop for the plots
for(i in 1:9){
plot(rnorm(i*5), 
main = "", 
xlab = "x",
ylab = "y", 
type = "p",
pch = 16,
col = "dodgerblue4")
}

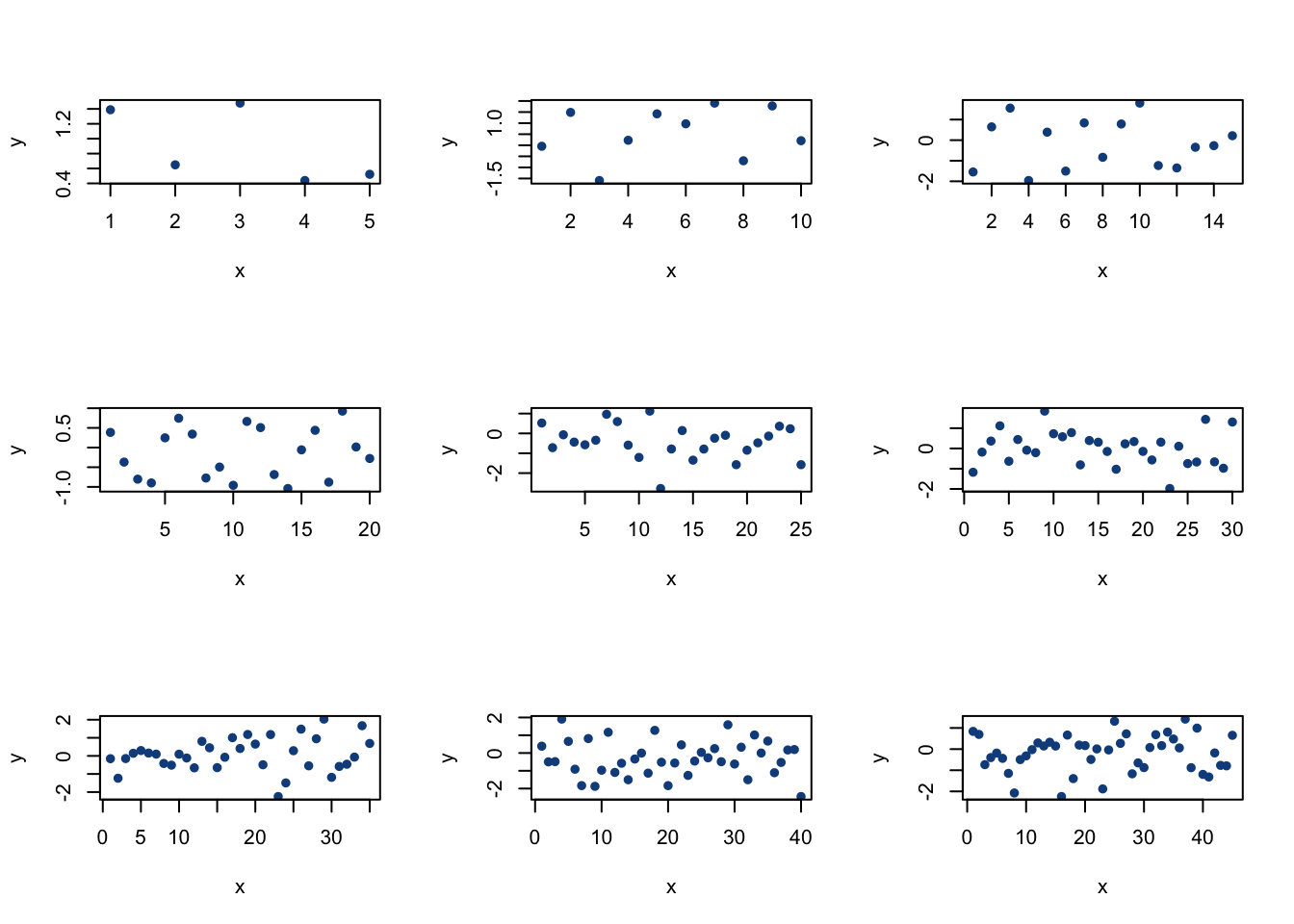
#restore the plot grid
par(mfrow = c(1,1))

par(mfrow = c(3,3))라는 코드는 R에게 그래프를 3×3 격자 형태로 배치하라고 지시하는 것이다. 첫 번째 플롯은 왼쪽 위 칸에 그려지고, 다음 그래프는 그 옆의 위쪽 가운데 칸에 그려지는 식으로, 9개의 칸이 모두 채워질 때까지 순서대로 들어간다. 이어서, for 루프를 실행하여 총 9번 반복하면서 매번 정규분포에서 추출한 값들을 플로팅하였다(그래프에서 보이는 것처럼 표본 크기가 점점 커진다). 마지막에는 par(mfrow = c(1,1))을 실행하여 그래픽 상태를 원래대로 복원해야 R이 다시 단일 플롯 영역으로 돌아간다는 것을 알 수 있다.

또한, 우리가 만든 플롯 위에 선을 추가하기 위해 abline 함수를 사용할 수도 있다. 다음 그래프를 보자.

#define vectors
x = seq(from = -10, to = 10, by = 1/10)
y = x^2
#plot
plot(x, y, 
main = "R Plot with Lines",
xlab = "x",
ylab = "y",
type = "l",
lwd = 4, 
col = "darkred",
ylim = c(min(y), max(y)),
xlim = c(-10, 10))
#draw lines
abline(v = 0,
lwd = 2,
col = "dodgerblue4")
abline(h = 40,
lwd = 2,
col = "dodgerblue4")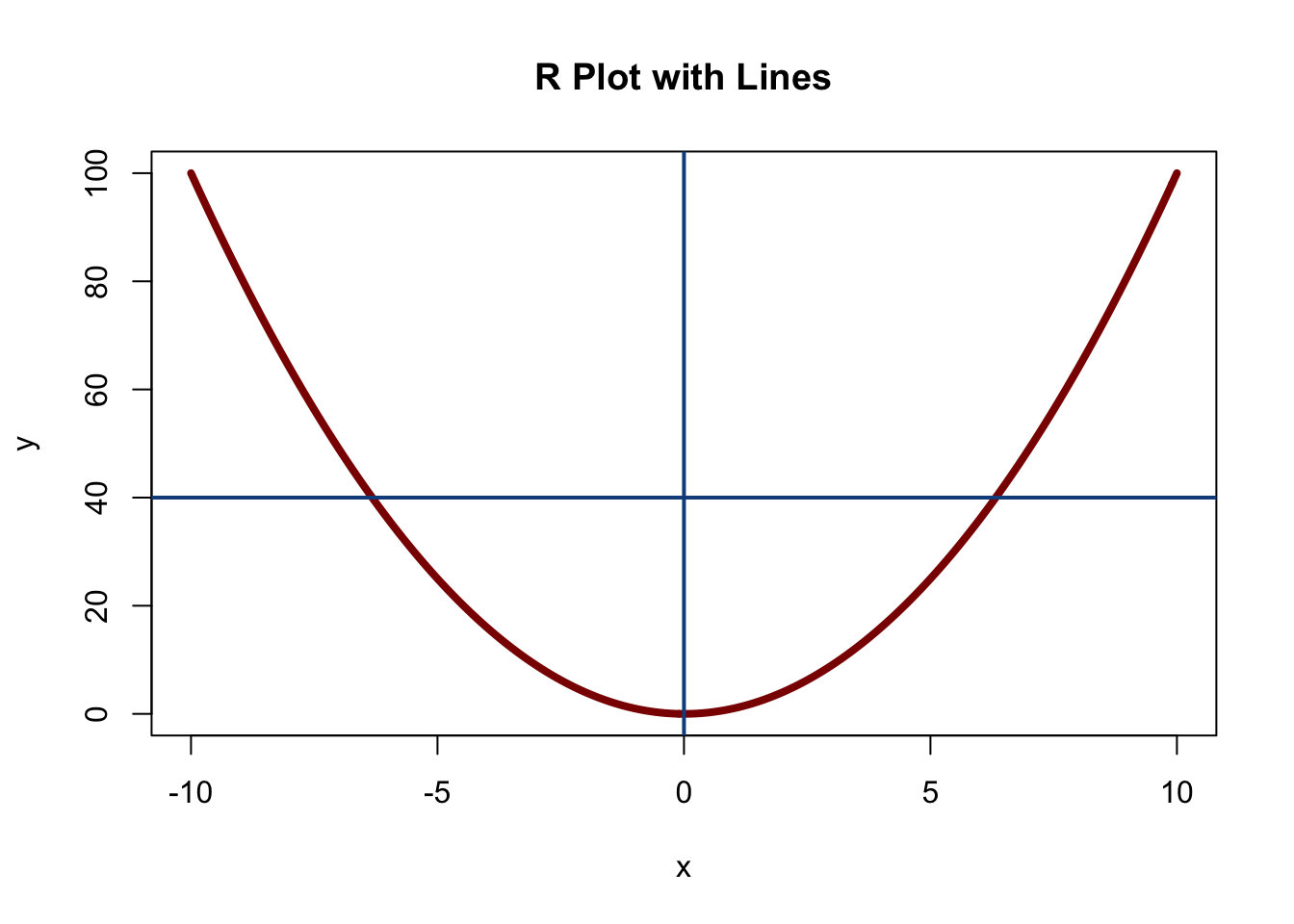

여기서는 먼저 플롯을 생성한 다음, 두 개의 선을 추가하였다. abline 함수는 plot 함수와 매우 비슷하여 col이나 lwd 같은 인자를 사용할 수 있지만, 가장 중요한 인자는 첫 번째 인자이다. 예를 들어, 여기서처럼 v = 5로 설정하면 x = 5 위치에 수직선을 그리겠다는 의미이고, h = 8로 설정하면 y = 8 위치에 수평선을 그리겠다는 의미이다.

• Getting help in R. R 함수, 패키지 등에 대한 도움말을 얻는 것은 보통 매우 쉽다. 콘솔에서 물음표 뒤에 도움말이 필요한 대상을 입력하기만 하면 되고, 만약 RStudio를 사용하고 있다면 오른쪽에 도움말 창이 나타난다.

?mean

• Commenting in R. 코드 블록 안에서 # 기호는 영어로 주석을 달 때 사용된다. 이는 사람이 코드를 읽을 때 무슨 일이 일어나고 있는지를 더 쉽게 이해할 수 있도록 돕는다(일반적으로 코드를 읽는 것은, 특히 다른 사람이 작성한 코드를 읽는 것은 매우 어렵다). R은 #으로 시작하는 줄을 건너뛰도록 되어 있다.

#This is a comment! R will not run this code.

• Downloading packages/libraries. 기본 R 패키지에는 유용한 기능이 많이 포함되어 있지만, 종종 기본 R 소프트웨어에 들어 있지 않은 기능이 필요할 때가 있다. 이러한 추가 ‘패키지’에는 우리가 특정 작업을 하기 위해 설치해야 하는 많은 유용한 도구들이 포함되어 있다. 필요한 코드를 포함한 패키지를 설치하려면 install.packages() 명령을 사용하고, 설치하려는 패키지 이름을 인자로 넣으면 된다(이때 반드시 따옴표로 묶어야 한다). 패키지는 한 번만 설치하면 된다. 그러나 패키지를 설치한 이후에는, 세션을 시작할 때 library() 명령을 사용해 해당 패키지를 불러와야 한다(이번에는 패키지 이름을 따옴표 없이 인자로 넣는다).
• Semi-colons. 코드 블록 사이에 세미콜론(;)을 사용하면 R이 출력 결과를 함께 보여준다.

#wihout a semi-colon
2 + 2

## [1] 4

2*2

## [1] 4

#with a semi-colon
2 + 2; 2*2

## [1] 4

## [1] 4

• Arithmetic calculations (sum, mean, etc.). 이러한 기본 명령어들 중 상당수는 R에 내장되어 있으며 사용하기 매우 간단하다. 이 부분은 뒤에서 다루겠지만, x = 1:3이라는 코드는 벡터 (1, 2, 3)을 x에 저장한다.

#define a vector
x = 1:3
#find the sum, mean and standard deviation
sum(x); mean(x); sd(x)

## [1] 6

## [1] 2

## [1] 1

• TRUE, FALSE R에서는 T를 TRUE로, F를 FALSE로 저장한다. 따라서 T라는 이름으로 어떤 것을 정의하는 것은 좋지 않은 습관이다(예: 벡터를 만들고 그것을 T라고 부르면 안 된다. 가능하다면 X와 같이 다른 이름을 사용하는 것이 좋다). 일반적으로 TRUE와 FALSE는 ‘if’ 문과 같은 조건문에서 사용된다.

#initialize x at 0
x = 0
#this should change x to 1
if(TRUE){
  x = 1
}
#print x
x

## [1] 1

• c(), or concatenation. 기본적으로, 이것은 객체들을 서로 묶어준다.

#bind 1 and 2 into a vector
c(1, 2)

## [1] 1 2

• NA. 이는 ‘not available(사용할 수 없음)’의 약자이다. 보통 우리는 벡터를 채우기 전에 NA로 먼저 채워 넣는다. R은 계산을 할 때 NA를 처리할 수 없는데, 예를 들어 NA가 들어 있는 벡터의 평균을 구할 수 없다. 이런 이유로 실제 데이터를 채우기 전에 벡터를 NA로 채워 두는 것이 좋은 습관이다. 만약 실수로 벡터의 특정 항목을 채우지 않았다면, 평균조차 구할 수 없기 때문에 R이 문제를 알려주게 된다.

#fill a vector with ten NA entries
x = rep(NA, 10)
#fill the vector with 1 to 10, incrementing by 1
#   search 'for loops' and 'indexing' for more info
for(i in 1:10){
  x[i] = i
}

• set.seed(). 컴퓨터에는 진정한 의미의 난수 생성이라는 것은 존재하지 않는다. 컴퓨터는 알고리즘을 실행하여 ‘의사 난수(pseudo-random)’를 생성한다. 우리는 이러한 알고리즘의 ‘seed(시드)’를 설정하여 ‘난수’ 과정에서 동일한 결과를 얻을 수 있으며, 이를 통해 코드를 다시 실행할 때 결과를 재현할 수 있다. 예를 들어:

set.seed(110)

이제 난수 과정을 시도해보자. 100개의 표준 균등분포 난수들의 평균을 구해보겠다.

mean(runif(100))

## [1] 0.5017964

이 코드를 다시 실행하면, runif가 ‘난수’를 생성하기 때문에 다른 값이 나온다.

mean(runif(100))

## [1] 0.4751529

그러나 다시 ‘seed’를 설정하면(그리고 같은 seed 값인 110을 사용하면), 처음 실행했을 때와 동일한 값을 얻을 수 있다.

set.seed(110)
mean(runif(100))

## [1] 0.5017964

이 해설 전반에서 우리가 사용한 것과 동일한 결과를 얻을 수 있도록 seed를 설정할 것이다. 여기서 사용할 ‘seed’ 값은 항상 110이다.

• runif. runif 함수는 지정된 구간에서 난수를 생성한다. 즉, 특정 개수 n의 난수를 하한값 min과 상한값 max 사이에서 추출한다(즉, Unif(a, b) 분포에서 추출하며, 여기서 a는 최소값, b는 최대값이다). 이러한 방식은 우리가 배우는 ‘대표적인’ 분포들에서도 거의 표준적으로 적용된다. 예를 들어, rnorm은 정규분포에서 난수를 생성할 수 있다(r은 random을 의미하고, unif는 uniform을 의미한다).

runif(n = 10, min = 0, max = 5)

##  [1] 1.9528672 0.4699530 3.4977928 4.6588981 1.1809279 1.9005877 2.3627924 0.7691976
##  [9] 1.6524571 2.8443326

runif(n = 10)

##  [1] 0.2836422 0.7407605 0.3658010 0.2006554 0.8325042 0.9261639 0.7242986 0.1317093
##  [9] 0.2777294 0.5944356

…이 함수는 기본적으로 최소값이 0이고 최대값이 1인 표준 균등분포를 사용한다(즉, 0과 1 사이에서 난수를 생성한다). 이는 R에서 ‘동전 던지기’나 유사한 확률적 사건을 시뮬레이션하는 데 매우 유용하다. 예를 들어, 표준 균등분포에서 값을 하나 생성한 뒤, 그 값이 0.5보다 크면 앞면(Heads), 0.5보다 작으면 뒷면(Tails)이라고 할 수 있다.

• ‘if’ statements, and/or logic. 이들은 다른 기본적인 코딩 언어들과 매우 유사한 유용한 논리문이다. 기본적으로 ‘if’ 명령문은 어떤 조건이 참인지 확인하고, 참일 경우 특정 동작을 수행한다. 예를 들어:

#check if 1 equals 1
if(1 == 1){
#set x equal to 10
  x = 10
}
#print x
x

## [1] 10

이는 “만약 1이 1과 같다면, x를 10으로 설정하라”는 의미이다. 실제로 1은 1과 같으므로, x는 10이 된다. 문법에서 주의할 점은 다음과 같다: 조건문에는 등호를 두 개(==) 사용해야 하고, 조건은 괄호 안에 들어가며, 실행할 동작(여기서는 x를 10으로 설정하는 것)은 중괄호 안에 들어간다.

또한, 논리 조건에 ‘and’와 ‘or’를 추가하여 더 복잡하게 만들 수도 있다.

#see if 1 equals 2 OR 2 equals 2
if(1 == 2 || 2 == 2){
  x = 10
}
#see if 1 equals 2 AND 2 equals 2
if(1 == 2 && 2 == 2){
  x = 20
}
#print x
x

## [1] 10

첫 번째 문장은 “만약 1이 2와 같거나(OR) 2가 2와 같다면, x = 10으로 설정하라”는 의미이다. 두 번째 문장은 “만약 1이 2와 같고(AND) 동시에 2가 2와 같다면, x = 20으로 설정하라”는 의미이다. 분명히 첫 번째 조건은 참이고 두 번째 조건은 거짓이므로, x에는 10이 저장된다.

큰 코드 블록을 실행할 때는 else와 else if 문을 포함시킬 수 있으며, 이는 동일한 구조를 기반으로 작성된다.

• Random Variables. 우리가 다루는 잘 알려진 분포 대부분은 이미 R에 구현되어 있다. 이러한 분포들로부터 난수를 쉽게 생성할 수 있고, 그 분포의 밀도 함수도 다룰 수 있다. 다음과 같은 대표적인 분포들의 도움말 페이지를 살펴보면 감을 잡을 수 있다. 일반적으로 r로 시작하는 함수(예: runif)는 난수를 생성하고, d로 시작하는 함수(예: dunif)는 특정 지점에서의 밀도 값을 반환한다. p로 시작하는 함수(예: punif)는 특정 지점까지의 분포의 누적분포함수(CDF)를 반환하며, q로 시작하는 함수(예: qunif)는 분위수(예: 분포의 50번째 백분위수에 해당하는 값)를 반환한다.

#Normal
?rnorm()
#Binomial/Bernoulli
?rbinom()
#Geometric
?rgeom()
#Exponential
?rexp()
#Beta
?rbeta()
#Gamma
?rgamma()
#Poisson
?rpois()
#Uniform
?runif()

• rep. 이는 지정된 길이와 값을 가진 벡터를 생성한다. 예를 들어:

x = rep(1, 5)

길이가 5이고 모든 값이 1로 채워진 벡터를 생성하여 x에 저장한다. 벡터는 다음과 같이 인덱싱할 수 있다.

x[3]

## [1] 1

이 코드는 벡터의 세 번째 값을 반환한다. 이 함수는 시뮬레이션을 채워 넣을 빈 경로를 설정할 때 매우 유용하다. 또한 벡터에서 특정 값을 제외하여 선택할 수도 있다.

x[-4]

## [1] 1 1 1 1

이 코드는 벡터 x에서 네 번째 요소를 제외한 모든 요소를 반환한다(모든 값이 동일하기 때문에 네 번째 요소가 빠졌다는 것을 알아차리기 어렵다!).

• matrix. 이 함수는 R에서 행렬을 생성하는 함수로, 값(data), 행의 개수(nrow), 열의 개수(ncol)를 지정할 수 있다. 예를 들어, 다음 명령어는 0으로 채워진 10×10 행렬을 생성하고 이를 x라고 한다.

x = matrix(data = 0, nrow = 10, ncol = 10)

이제 행렬의 i번째 행, j번째 열의 값을 다음과 같이 인덱싱하여 접근할 수 있다.

x[4, 5]

## [1] 0

이는 x의 4번째 행, 5번째 열에 있는 요소를 가져오는 것이다(이 행렬의 모든 값이 0이기 때문에 올바른 값을 선택했는지 구분하기는 어렵다). 이 함수는 시뮬레이션을 채워 넣을 빈 경로를 설정할 때 매우 유용하다.

• rbind and cbind. 각각 ‘행 결합(row bind)’과 ‘열 결합(column bind)’을 의미한다. 이 함수들은 구조들을 행 또는 열 단위로 묶어주며, 여러 벡터나 행렬을 다룰 때 유용하다.

#define two matrices
matrix0 = matrix(0, nrow = 3, ncol = 3)
matrix1 = matrix(1, nrow = 3, ncol = 3)
#bind by rows (top and bottom)
rbind(matrix0, matrix1)

##      [,1] [,2] [,3]
## [1,]    0    0    0
## [2,]    0    0    0
## [3,]    0    0    0
## [4,]    1    1    1
## [5,]    1    1    1
## [6,]    1    1    1

#bind by column (side by side)
cbind(matrix0, matrix1)

##      [,1] [,2] [,3] [,4] [,5] [,6]
## [1,]    0    0    0    1    1    1
## [2,]    0    0    0    1    1    1
## [3,]    0    0    0    1    1    1

• data.frame (in the data.table package). 이는 어떤 데이터 객체(보통 행렬)를 데이터 프레임(data frame)으로 변환한다. 예를 들어:

#create the matrix 
x = matrix(runif(20), nrow = 10, ncol = 2)
#convert to a data frame
x = data.frame(x)

여기서는 10행 2열(10×2)의 행렬 x를 만들고, 균등분포에서 추출한 20개의 난수로 채웠다. 그런 다음 x를 data.frame으로 변환하였다.

데이터 프레임의 장점 중 하나는 특정 유형의 객체에 대해 주요 작업을 보다 쉽게 수행할 수 있다는 점이다. 예를 들어, 여기서 남성 10명과 여성 10명의 데이터를 수집했다고 가정해보자(따라서 열이 2개). 이때 남성 집단의 평균을 구하려고 한다면, 행렬에서는 올바른 인덱스를 지정해야 하지만, 데이터 프레임에서는 훨씬 더 쉽게 처리할 수 있다.

먼저 colnames 명령을 이용해 열 이름을 지정할 수 있다. rownames 명령은 동일한 기능을 행 이름에 대해 수행한다.

#name the columns
colnames(x) = c("Men", "Women")

원한다면 x를 확인해 보라. 이전과 동일하지만 열 이름이 추가되어 있을 것이다. 이제 달러 기호($) 연산자를 사용하여 그 열 이름에 접근할 수 있다.

#grab the 'Men' column
x$Men

##  [1] 0.113263783 0.136841874 0.869321317 0.571819524 0.002760004 0.866104885 0.216270895
##  [8] 0.738721495 0.557044378 0.441975039

이는 데이터 프레임에서 Men 열 벡터를 가져오는 것이다. 이제 이를 이용해 남성 집단의 평균을 구하는 것과 같은 다양한 연산을 수행할 수 있다.

mean(x$Men)

## [1] 0.4514123

이 열은 특별한 방식으로도 인덱싱할 수 있다. 예를 들어, 남성 집단의 평균을 구하되 같은 시도(같은 행)에서 여성 집단의 데이터가 0.5보다 큰 경우만 포함하고 싶다고 하자. 이때는 다음과 같이 하면 된다:

mean(x$Men[x$Women > .5])

## [1] 0.1368419

여기서 mean 함수 안의 코드는 데이터 프레임 x에서 남성 집단의 벡터를 반환한다. 구체적으로는, 여성 집단의 해당 값이 0.5보다 큰 경우에만 남성 집단의 값을 인덱싱하여 가져온 것이다.

• unique. 함수는 벡터에서 고유한 요소들을 반환한다. 이는 시뮬레이션에서 매우 유용한데, 종종 우리는 고유한 벡터의 길이에 관심을 가지기도 한다.

#define a vector
# remember, we use 'c()' to concatenate, or bind
vector1 = c("a", "a", "b", "c", "c", "d")
#there are 4 unique elements: "a", "b", "c" and "d"
unique(vector1)

## [1] "a" "b" "c" "d"

• length. 객체(보통 벡터)의 길이를 반환한다. 이는 벡터에서 특정 조건을 만족하는 값이 몇 개인지 확인할 때 매우 유용하다.

#define this vector, which has 3 elements (length 3)
vector1 = c(5, 2, 4)
length(vector1)

## [1] 3

#draw 10 values from a standard normal, count how many are negative
X = rnorm(10)
length(X[X < 0])

## [1] 6

아래 줄에서는 평균 0, 분산 1의 정규분포 $N(0,1)$에서 10개의 값을 추출하여 벡터 X에 저장한다. 코드 X[X < 0]는 X에서 값이 0보다 작은 원소들만을 뽑아 부분 벡터로 반환하며, 이 부분 벡터의 길이를 구하면 X에서 음수인 값이 몇 개인지를 셀 수 있다.

• paste0. 본질적으로 ‘concatenate’ 함수와 동일하지만 문자열(즉, 텍스트로 이루어진 객체)에도 적용된다. c() 함수처럼 인자들은 쉼표로 구분한다.

#generate a random number
X = rnorm(1)
#print out a sentence
paste0("I generated the random number ", X, ".")

## [1] "I generated the random number -0.63180229621031."

이는 우리가 위에서 했던 것처럼 난수 시뮬레이션의 결과를 출력하고자 할 때 유용하다.

• sample. 원하는 벡터에서 표본을 추출하는 매우 유용한 함수이다. 또한 매우 다재다능한 함수이다. 첫 번째 인자는 표본을 추출할 벡터이고, 두 번째 인자인 size는 추출할 표본의 개수를 지정한다. 세 번째 인자인 replace를 통해 복원 추출 여부를 결정할 수 있으며, 네 번째 인자인 prob은 표본의 확률질량함수(PMF)를 지정한다.

#replicate
set.seed(110)
#generate a random iteration of the vector 1,2,...,5
sample(1:5)

## [1] 4 1 3 2 5

#sample 3 values from the vector 1,2,...,5 without replacement
sample(1:5, 3)

## [1] 1 4 3

#sample 7 values from the vector 1,2,...,5 with replacement
sample(1:5, 7, replace = TRUE)

## [1] 4 3 4 1 3 4 5

#sample 7 values from the vector 1,2,...,5 with replacement
#and with a specific PMF
sample(1:5, 7, replace = TRUE, prob = c(.3, .3, .3, .1, 0))

## [1] 2 2 3 3 3 4 3

이 예시들은 sample 함수가 점점 더 복잡하게 사용되는 모습을 보여준다. 만약 replace와 prob 인자를 지정하지 않으면, replace의 기본값은 FALSE(즉, 비복원 추출)이고, prob의 기본값은 균등분포(모든 값이 동일한 확률로 선택됨)이다. 마지막 예제에서는 prob 인자에 벡터를 설정하여 사용자 정의 PMF를 지정했다. 이는 각 추출에서 1은 확률 0.3, 2는 확률 0.3 등으로 선택된다는 것을 의미한다. 결과를 보면 2와 3이 많이 선택되고, 5는 전혀 나오지 않는데, 이는 우리가 정의한 PMF에서 5의 선택 확률을 0으로 설정했기 때문이다.

• : 연산자는 두 숫자 사이에서 사용되며, 두 숫자 사이의 값을 1씩 증가하는 벡터로 반환한다.

#vector from 1 to 10, with steps of 1
1:10

##  [1]  1  2  3  4  5  6  7  8  9 10

#can also increment across numbers with decimals
4.7:8.7

## [1] 4.7 5.7 6.7 7.7 8.7

• seq 함수는 수열을 생성한다. 첫 번째 인자인 from으로 시작점을, 두 번째 인자인 to로 끝점을 지정할 수 있으며, 증가 간격은 by(특정 값만큼 증가)나 length.out(수열의 길이를 강제로 지정)으로 설정할 수 있다.

#create a vector from 1 to 10, increment by 1
seq(from = 1, to = 10, by = 1)

##  [1]  1  2  3  4  5  6  7  8  9 10

#create a vector from 20 to 30, with length 30
seq(from = 20, to = 30, length.out = 30)

##  [1] 20.00000 20.34483 20.68966 21.03448 21.37931 21.72414 22.06897 22.41379 22.75862
## [10] 23.10345 23.44828 23.79310 24.13793 24.48276 24.82759 25.17241 25.51724 25.86207
## [19] 26.20690 26.55172 26.89655 27.24138 27.58621 27.93103 28.27586 28.62069 28.96552
## [28] 29.31034 29.65517 30.00000

• round 함수는 첫 번째 인자인 값을 두 번째 인자로 지정한 소수점 자리까지 반올림한다. 이는 R이 매우 많은 소수 자릿수까지 난수를 생성하기 때문에 유용하게 사용될 수 있다.

#round a random normal draw
round(rnorm(1), 2)

## [1] 0.97

• sort 함수는 첫 번째 인자인 벡터를 오름차순 또는 내림차순으로 정렬한다. 두 번째 인자인 decreasing을 FALSE 또는 TRUE로 설정하여 방향을 지정할 수 있으며, 기본값은 오름차순 정렬이다.

#create a vector
vector1 = c(1,2,3)
#sort the vector in two ways
sort(vector1)

## [1] 1 2 3

sort(vector1, decreasing = TRUE)

## [1] 3 2 1

• rev 함수는 벡터를 입력받아 그 순서를 반대로 뒤집어 반환한다.

#define a vector
vector1 = c(1,2,3)
#reverse it
rev(vector1)

## [1] 3 2 1

• Indexing (square brackets: [ ]). 앞에서 보았듯이, 대괄호를 사용하여 벡터를 인덱싱할 수 있다. 이를 조금 더 확장하면, 벡터를 인덱싱하면서 특정 조건을 만족하는 값들만 선택할 수도 있다.

#create a new vector from 1 to 5
x = 1:5
#select values in the vector that are less than 2
x[x < 2]

## [1] 1

이는 벡터 x에서 인덱스 조건을 만족하는 모든 값을 선택한다. 여기서는 값이 2보다 작은 경우만 선택된다. 이 함수는 R의 ‘and/or’ 논리를 사용하여 더 복잡하게 만들 수 있으며, 인덱싱 대괄호 안에서는 & 하나만 사용한다는 점에 유의해야 한다.

x[x > 2 & x < 5]

## [1] 3 4

이는 벡터 x에서 값이 2보다 크고 5보다 작은 모든 값을 선택한다.

• Graphics. 다음 명령어들은 R에서 유용하고 사용자 지정 가능한 그래프를 생성하는 데 도움을 준다. 각 함수가 어떻게 작동하는지 확인하려면 도움말 페이지를 살펴보면 된다.

#standard plots
?plot
#histograms
?hist
#add another series to a plot
?lines
#add straight lines to a chart
?abline
#create a legend for a plot
?legend

• sapply는 매우 유용한 함수로, 보통 ‘for loop’를 사용할 만한 상황에서 자주 쓰인다. 이 함수는 어떤 함수를 벡터 전체에 적용할 수 있게 해준다. 예를 들어, 큰 벡터 X가 있고 그 안의 각 값의 제곱을 구하고 싶다고 하자. 이때 sapply를 사용하면, 지정한 함수(여기서는 제곱 함수)를 벡터의 각 값에 적용할 수 있다.

#generate a vector for X
X = rnorm(100)
#calculate the square of X
Y = sapply(X, function(x) x^2)

여기서 sapply의 첫 번째 인자는 우리가 반복 적용하고자 하는 대상, 즉 X이다. 두 번째 인자는 우리가 적용하고자 하는 함수이며, 이는 일반적으로 함수를 정의하는 방식대로 작성한다. 즉, function(x)라고 쓴 뒤, 그 안에 x의 제곱을 계산하는 함수를 넣는다. 여기서 소문자 x를 사용한 것은 중요하지 않다. 일관성만 유지된다면 어떤 문자를 사용해도 된다.